第1讲 相交线
Ⅰ、相交线
邻补角：有一条________，另一条边互为_________的两个角叫做邻补角。
对顶角：有一个公共的_________，两边分别____________的两个角叫做对顶角。
邻补角_________，对顶角________。
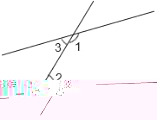
1.如图所示,∠1和∠2是对顶角的图形有（ ）
2.下列说法正确的有
①对顶角相等; ②相等的角是对顶角; ③若两个角不相等,则这两个角肯定不是对顶角;
④若两个角不是对顶角,则这两个角不相等.
A.1个 B.2个 C.3个 D.4个
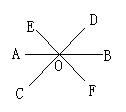
3.如图所示,三条直线AB,CD,EF相交于一点O,则∠AOE+∠DOB+∠COF等于
A.150° B.180° C.210° D.120°
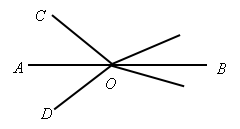
如图4所示,已知直线AB,CD相交于O,OA平分∠EOC,∠EOC=70°,则∠BOD=______.
5.如图5所示,直线AB,CD相交于点O,若∠1-∠2=70°,则∠BOD=_____,∠2=_______.
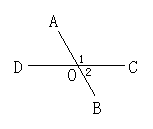
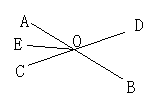
（4）
6.如图6所示,直线AB,CD相交于点O,OE平分∠AOC,若∠AOD-∠DOB=50°,则∠EOB=______.
7.如图，直线AB、CD相交于点O，∠AOC=80°，OE把∠BOD分成两部分，且∠BOE：∠EOD=2:3，求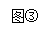
∠AOE的大小。
8.已知直线AB、CD相交于点O，OE平分∠BOD，OF平分∠COE，∠2=4∠1，求∠AOF的度数。
9.找规律
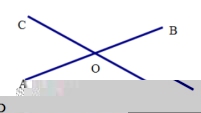
（1）察看图①，图中共有______条直线，_________对对顶角，__________对邻补角
（2）察看图②，图中共有______条直线，_________对对顶角，__________对邻补角
（3）察看图③，图中共有______条直线，_________对对顶角，__________对邻补角
（4）若有n条不一样的直线相交于一点，则可以形成_________对对顶角，__________对邻补角
Ⅱ、垂线的性质
1.在同一平面内，过一点有且仅有________直线与已知直线垂直。
2.连接直线外一点与直线上各点的所有线段中，垂线段________，可简说成______________
3.直线外一点到这条直线的垂线段的长度，叫做________________
作图：垂线及垂线段的画法
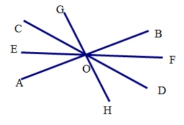
已知一点M及∠AOB，过M点作OA，OB的垂线，垂足分别为E、F。
训练：1．在两条直线相交所成的四个角中，不可以断定这两条直线垂直。
A．对顶角互补 B．四对邻补角 C．三个角相等 D．邻补角相等
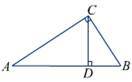
2．如图，在三角形ABC中，AC⊥BC，CD⊥AB于D，则下列关系不成立的是
A．AB>AC>AD B．AB>BC>CD C．AC+BC>AB D．AC>CD>BC
3.如图所示,下列说法不正确的是
A.点A到BC的垂线段是线段AC; B.点B到AC的垂线段是线段BC
C.线段CD是点D到AB的垂线段; D.线段AD是点A到CD的垂线段
4.下列说法正确的有
①在平面内,过直线上一点有且只有一条直线垂直于已知直线;②在平面内,过直线外一点有且只有一条直线垂直于已知直线;③在平面内,过一点可以任意画一条直线垂直于已知直线;④在平面内,有且只有一条直线垂直于已知直线.
A.1个 B.2个 C.3个 D.4个
5.直线
外有一点P，它到直线m上三点A，B，C的距离分别是6cm，3cm，5cm，则点P到直线的距离为（ ）
A、3cm B、5cm C、6cm D、不大于3cm
6.在三角形ABC中，AC⊥BC，CD⊥AB于D，AC=4，BC=3，AB=5，如图，则在图中共有______对互余的角，______对互补的角，______对邻补角，点A到BC的距离是______，到点B的距离是______，点C到直线AB的距离是______．
7．如图，已知直线AB、CD、EF相交于O，OG⊥AB，且∠FOG = 32º，∠COE = 38º，求∠BOD．
8.如图，直线AB，CD相交于点O，EO⊥AB于点O，∠EOD=50°，求∠BOC的度数。
9.如图所示，直线AB，CD相交于点O，作∠DOE=∠BOD，OF平分∠AOE.
判断OF与OD的地方关系；
若∠AOC:∠AOD=1:5，求∠EOF的度数。
Ⅲ、三线八角
同位角：在两条被截直线的________，并且在截线的________，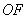 
3.如图，直线a、b被直线AB所截，且AB⊥BC， ∠1和∠2是_______角； 若∠1与∠2互补，则∠1-∠3=_______.
4.如图，图中有________对同位角，________对内错角，________对同旁内角．
5.两条直线被第三条直线所截，∠1是∠2的同旁内角，∠3是∠2的内错角.
（1）依据上述条件画出示意图；
（2）若∠1=3∠2，∠2=3∠3，,求∠1、∠ 2的度数.
6.如图，直线
相交于，平分
，求度数.
7.如图，直线
经过点，
平分
平分
求
的度数； 
判断
与
的地方关系，并说明理由. 综合题练习（选讲）：
1、已知点O为直线AB与直线CF的交点，∠BOC=α.
（1）如图1，若α=40°，OD平分∠AOC，∠DOE=90°，求∠EOF的度数；
（2）如图2，若∠AOD=
∠AOC，∠DOE=60°，求的度数（用含α的式子表示）.
2、已知OA⊥OB，OC⊥OD.
如图①,若∠BOC=50°，求∠AOD的度数；
如图②,若∠BOC=60°，求∠AOD的度数；
依据结果猜想∠AOD与∠BOC有什么样的关系?并依据图①说明理由；
如图②，若∠BOC:∠AOD=7:29，求∠COB和∠AOD的度数。
作业：
1.画图并填空：如图，请画源于A地经过B地去河边l的最短路线。
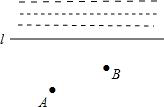
确定由A地到B地最短路线的依据是___________________________.
确定由B地到河边l的最短路线的依据是___________________________________.
2.
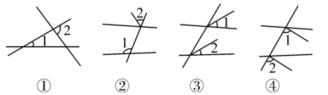如图，∠1和∠2是同位角的是（ ）
3.在如图中按需要画图。
（1）过B画AC的垂线段；
（2）过A画BC的垂线；
（3）画出表示点C到AB的距离的线段。
4.如图,直线AB,CD相交于点O,OE平分∠BOD,OE⊥OF,∠DOF=70∘，求∠AOC的度数。
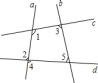
5.如图，在图中用数字表示的几个角中，∠1与______是同位角，∠3与______是同旁内角，∠2与______是内错角。
6.如图，∠3的同旁内角是______，∠4的内错角是______，∠7的同位角是______.
相交线答案
Ⅰ、相交线
邻补角：有一条公共边，另一条边互为反向延长线的两个角叫做邻补角。
对顶角：有一个公共的顶点，两边分别互为反向延长线的两个角叫做对顶角。
性质：邻补角互补，对顶角相等。
B
B
B
35°
125°；55°
147.5°
148°
108°
9.（1）2，2，4 （2）3，6，12 （3）4，12,24 （4）n（n-1）,2n（n-1）
Ⅱ、垂线的性质
1.在同一平面内，过一点有且仅有_________________直线与已知直线垂直。
2.连接直线外一点与直线上各点的所有线段中，垂线段___________，可简说成_____________
3.直线外一点到这条直线的垂线段的长度，叫做______________
做图:略
训练：
1.B 2.D 3.C 4.C 5.D 6.4,3,1 ， 4,5，
20° 8. 140° 9.（1）OF⊥OD （2）60°
Ⅲ、三线八角
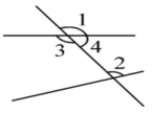同位角：在两条被截直线的______________，并且在截线的______________________________，
如图中∠1与∠_____________就是同位角。
内错角：在_____________之间，并且在截线的________________________，
如图中∠2和______________就是内错角。
同旁内角：在______________之间，并且在截线的________________，
如图中∠2和________________就是同旁内角。
训练：
D
2.①DE，BC，内错 ②EC,BC,同旁内角 ③BE,BA，同位 ④∠ABE和∠BEC,∠ABE和∠AEB ⑤∠ADE和∠ABC,∠EDB和∠DBC
3.（1）同旁内 （2）90°（提示：∠1+∠2=180①，∠2＋∠3=90②，①－②得，∠1-∠3=90°）
4. 12,6,6（提示：一组三线八角基础图形有4对同位角，2对内错角，2对同旁内角，这里有三组）
5.（1）如图所示：
∠1=162°,∠2=54°
6. 105°
7.（1）90° （2）OD⊥ON
综合题练习（选讲）：
1.（1）20° （2）
2.（1）130° （2）120° （3）∠AOD+∠BOC=180° （4）∠COB=35°，∠AOD=145°
作业：
1.作图略
确定由A地到B地最短路线的依据是__两点之间，线段最短__.
确定由B地到河边l的最短路线的依据是____垂线段最短_____.
2.C
3.略
4.40°
5.∠4，∠1、∠5，∠1
6.∠4、∠5；∠2；∠1、∠4
